벨만 포드 알고리즘 (Bellman-Ford algorithm) - soo:bak

작성일 :

개념

  • 시작 노드 에서 그래프의 다른 모든 노드 로 가는 최단 경로는 구하는 알고리즘

특징

  • 경로의 길이가 음수인 사이클 을 포함하지 않는 모든 종류의 그래프를 처리할 수 있음
  • 만약, 그래프에 경로의 길이가 음수인 사이클 이 있는 경우, 이를 찾아낼 수도 있음
  • 노드의 개수를 n , 간선의 개수를 m 이라고 할 때, 해당 알고리즘은 n - 1 의 단계로 구성됨
  • 단계마다 m 개의 간선을 모두 처리하므로, 시간 복잡도는 O(nm)

설명

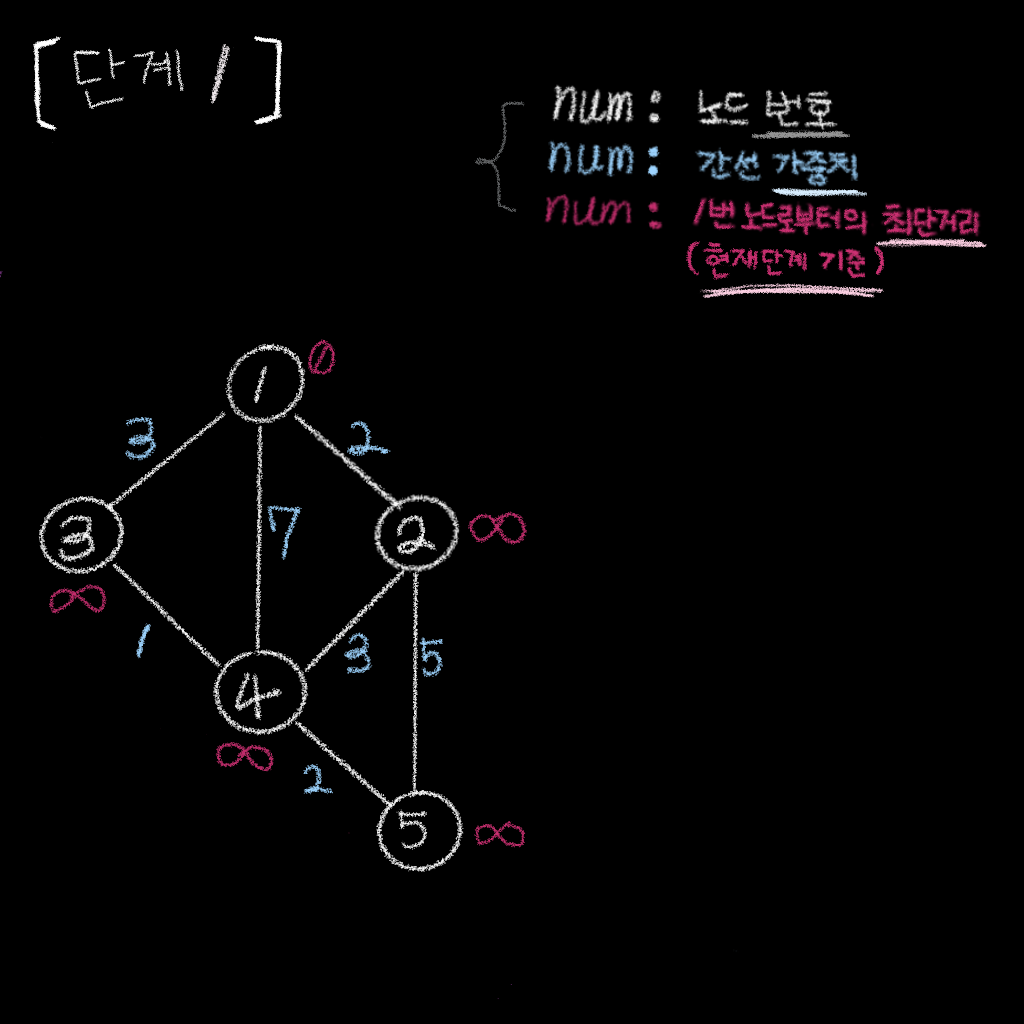단계 1

단계 1  .  거리의 초깃값을 설정

  • 시작 노드의 거리값은 0
  • 다른 모든 노드의 거리값은 무한대




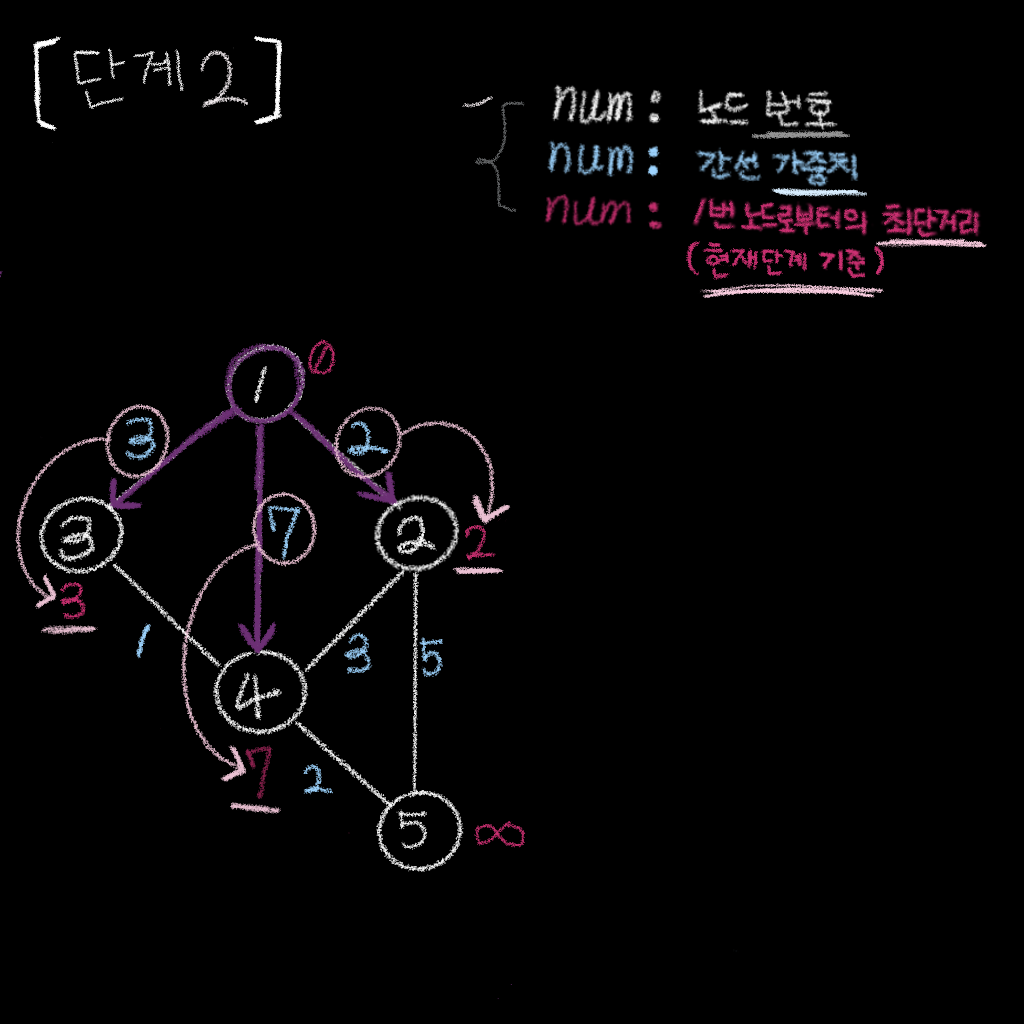단계 2

단계 2  .  시작 노드로부터의 간선들을 이용하여, 연결되는 노드들의 거리값을 줄임

  • 노드 1   ->  노드 2   간선의 거리는 2 이므로, 노드 2 의 거리값은 2
  • 노드 1   ->  노드 3   간선의 거리는 3 이므로, 노드 3 의 거리값은 3
  • 노드 1   ->  노드 4   간선의 거리는 7 이므로, 노드 4 의 거리값은 7




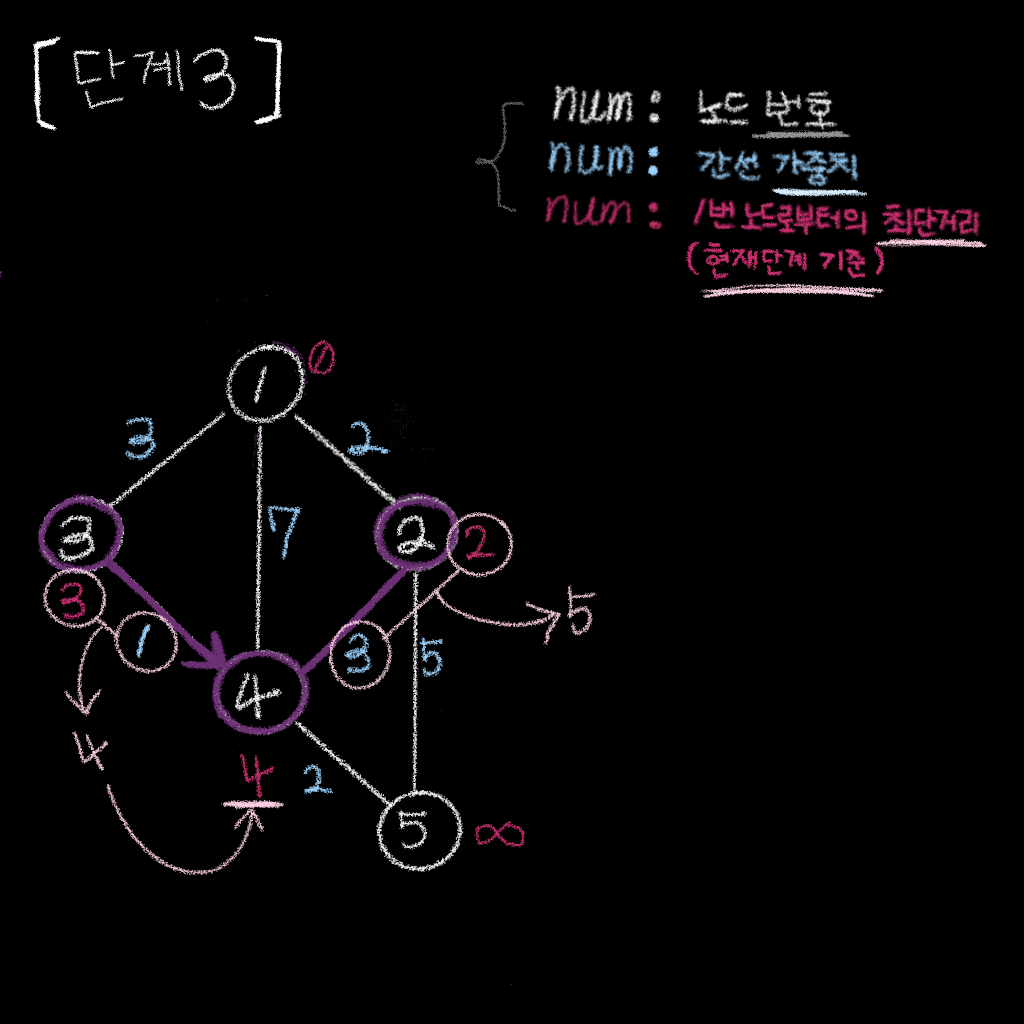단계 3

단계 3  .  이제 다음 단계의 간선들을 이용하여 각 노드의 거리값을 줄임

  • 단계 2 에서 기존 노드 4 의 거리값은 7
  • 노드 2 의 거리값은 2, 노드 2   ->   노드 4   간선의 거리는 3, 합은 5
  • 노드 3 의 거리값은 3, 노드 3   ->   노드 4   간선의 거리는 1, 합은 4
    • 따라서, 노드 3   ->  노드 4   거리값 4 가 가장 작으므로, 노드 4  의 거리값을 4 로 줄임




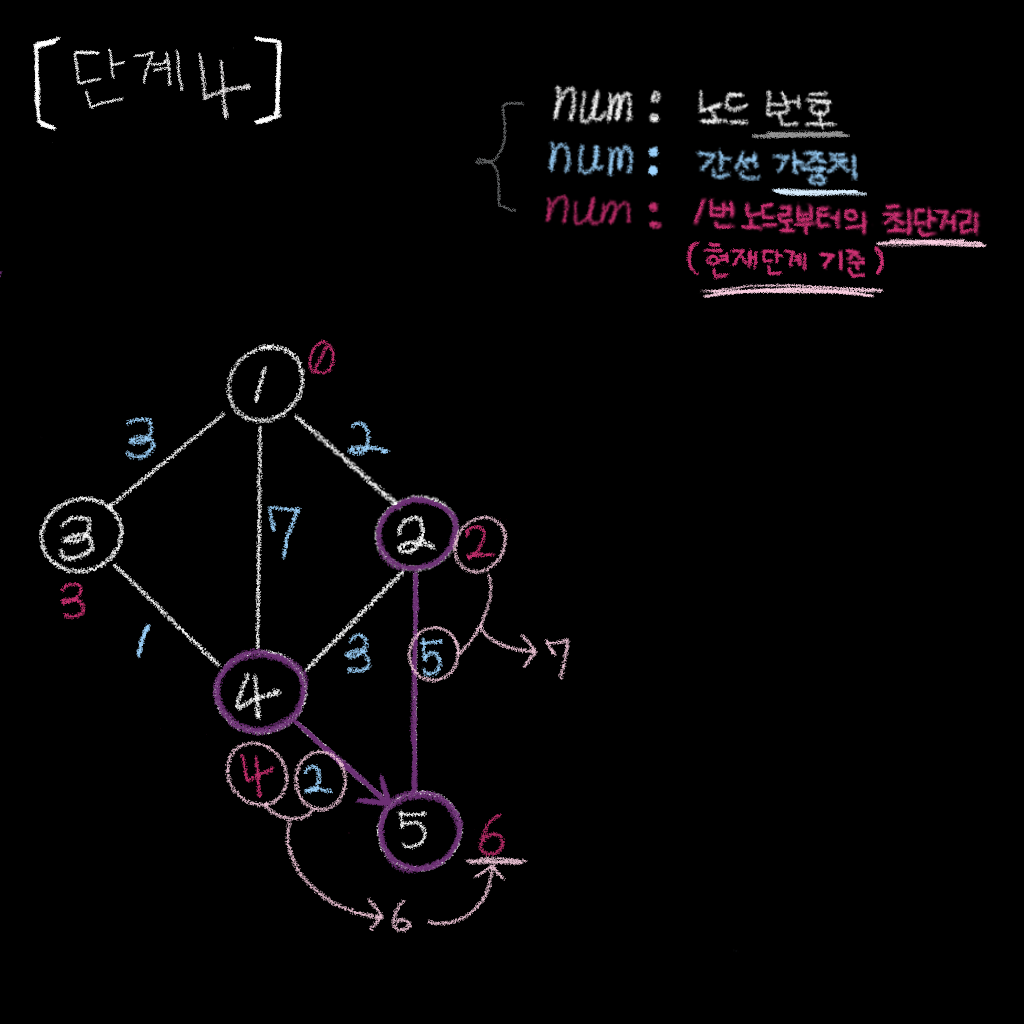단계 4

단계 4  .  또 다음 단계의 간선들을 이용하여 각 노드의 거리를 줄임

  • 노드 2 의 거리값은 2, 노드 2   ->   노드 5   간선의 거리는 5, 합은 7
  • 노드 4 의 거리값은 4, 노드 4   ->   노드 5   간선의 거리는 2, 합은 6
    • 따라서, 노드 4   ->  노드 5   거리값 6 이 가장 작으므로, 노드 5  의 거리값을 6 으로 줄임




종결

종결

  • 이후에는 거리값들을 더 이상 줄일 수 없기에, 이렇게 구한 값이 최종 거리가 됨


설명 요약

  • 시작 노드 에서 다른 모든 노드 까지의 거리값을 추적
  • 각 단계에서의 노드 로부터 모든 간선 을 살펴보며, 해당 간선이 거리값을 줄이는 데에 사용될 수 있는 지 확인
  • 만약 거리값을 줄일 수 있다면, 해당 노드까지의 거리값을 줄여진 거리값으로 갱신
  • 위의 과정을, 각 노드 별 거리값을 더이상 줄일 수 없을 때 까지 반복


음수 사이클

  • 그래프에 음수 사이클이 있는 경우를 제외하면, n - 1 번의 단계가 끝난 후 모든 노드에 대해서 최종 거리값을 구할 수 있게 됨
    • 각각의 최단 경로가 포함하는 간선의 수가 최대 n - 1 개 이기 때문
  • 음수 사이클의 존재 여부 확인
    • 만약 그래프에 음수 사이클이 존재한다면, 사이클을 포함하는 경로의 길이는 무한히 짧아질 수 있기 때문에, 최단 경로를 구하는 것은 의미가 없음 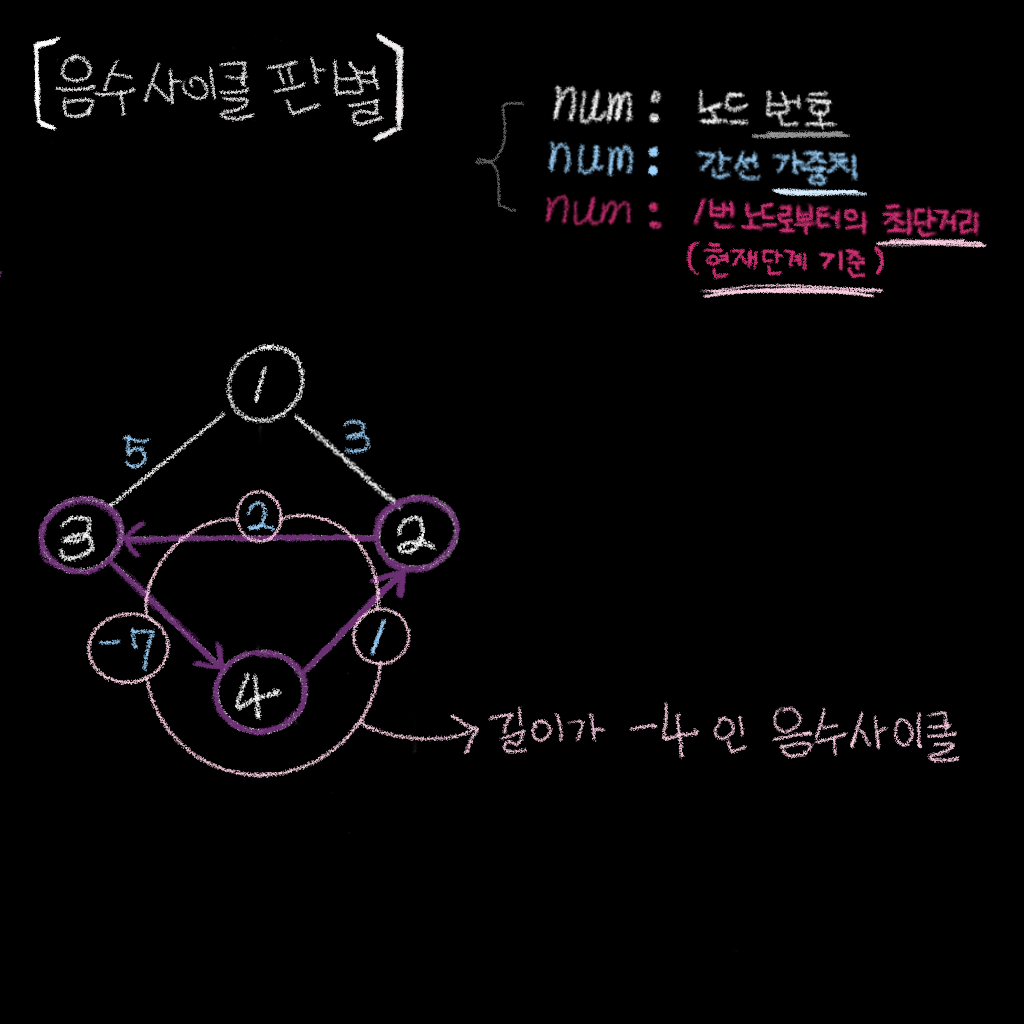음수 사이클
      • 위 그림에서, 노드 2   ->  노드 3   ->  노드 4   ->  노드 2   사이클은 길이가 -4 인 음수 사이클 임


    • 벨만-포드 알고리즘을 n 번의 단계로 진행한다면, 음수 사이클의 존재를 찾을 수 있음
      • 마지막 단계에서도 거리값이 줄어드는 경우가 있다면, 그래프에 음수 사이클이 존재한다는 것이기 때문
      • 이 방법을 이용하면 시작 노드를 어떤 노드로 설정하더라도, 그래프의 음수 사이클 존재 여부를 확인할 수 있음

구현

  • 그래프는 보통 가중치가 포함된 간선 리스트를 이용

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

    /* 각 노드의 거리값을 담을 배열 dist[] 선언 */

for (int i = 1; i <= n; i++)
  dist[i] = INF;

int numStartNode = 1;
/* 보통 문제의 조건에 따라 시작 노드를 변경하게 되므로, 설명을 위해 임의의 노드 1을 시작 노드로 선언하였음 */
dist[numStartNode] = 0;

for (int i = 0; i <= n - 1; i++) {
  for (auto e : edges) {
    int from, to, w;
    tie(from, to, w) = e;
    if (dist[from] = INF) continue ;
    dist[to] = min(dist[to], dist[from] + w);
  }
}



최적화

  • 방법 1
    • 보통의 경우 n - 1 번 단계를 진행하기 전에 모든 노드들의 최종 거리값이 계산 됨
    • 한 단계를 진행하는 동안, 거리값이 줄어드는 경우가 없었다면, 알고리즘을 즉시 종료하여도 됨
      • 예시 - 각각의 단계마다 거리값이 줄어들었는 지 체크한 후, 거리값이 줄어들지 않았다면 알고리즘 종료
      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

      typedef long long ll;

vecotr<ll> dist(NODE_MAX, INF);
bool isNegCycle = false;
/* 만약, n 번째 단계에서 거리값이 줄었다면,
   그래프에 음수 사이클이 존재하는 경우일 수도 있으므로
   이를 체크하기 위한 변수 */

for (int i = 1; i <= cntNode; i++) {
  bool isDecreased = false;
  /* 거리값이 줄어들었는 지 체크하기 위한 변수 */

  for (auto e : edges) {
    int from, to, w;
    tie(from, to, w) = e;
    if (dist[from] == INF) continue ;
    if (dist[to] > dist[from] + w) {
      isDecreased = true;
      if (i == cntNode) isNegative = true;
      else dist[to] = min(dist[to], dist[from] + w);
    }
  }
  if (!isDecreased) break ;
  /* 해당 단계에서 거리값이 줄어들 지 않았다면,
     알고리즘 종료 */
}


  • 방법 2
    • SPFA(Shortes Path Faster Algorithm, 좀 더 빠른 최단 경로 알고리즘) 활용
    • 해당 알고리즘은 거리값을 줄이는 데에 사용 될 수 있는 노드들을 별도의 큐 로 관리
    • 큐로 관리되는 노드만 처리함으로써, 보다 더 효율적인 탐색 진행 가능

이 블로그의 다른 글