피보나치 수열 (Fibonacci Sequence) - soo:bak
작성일 :
피보나치 수열이란?
피보나치 수열(Fibonacci Sequence) 은 수학, 컴퓨터 과학, 자연과학 등 다양한 분야에서 등장하는 수열입니다.
수열은 단순한 규칙으로 구성되지만, 다양한 이론적, 실용적 응용이 가능합니다.
피보나치 수열은 다음과 같이 정의됩니다:
\[F(0) = 0, \quad F(1) = 1 \\ F(n) = F(n-1) + F(n-2) \quad \text{for } n \geq 2\]즉, 각 항은 앞선 두 항의 합으로 결정되며, 이 규칙을 반복하여 수열이 확장됩니다.
피보나치 수열의 전개
피보나치 수열의 초반 항들을 나열하면 다음과 같습니다:
\[0,\ 1,\ 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,\ 55,\ 89,\ 144,\ \dots\]수열이 전개되면서 항의 크기는 점점 커지며, 각 항이 앞선 두 항의 합으로 이루어지는 패턴을 유지합니다.
또한, 항이 커질수록 두 인접 항의 비율은 일정한 값으로 수렴하는 성질도 확인할 수 있습니다.
피보나치 수열 계산 방법
피보나치 수열을 계산하는 방법은 다양한 접근이 가능합니다.
1. 재귀적 구현 (Recursive)
수열의 정의를 그대로 반영한 가장 직관적인 방법입니다.
기본 재귀 구현
1
2
3
4
int fibonacci(int n) {
if (n <= 1) return n;
return fibonacci(n - 1) + fibonacci(n - 2);
}
- 장점: 구현이 간결하고 수열의 수학적 구조를 직접 표현합니다.
- 단점: 중복 계산이 많아 시간 복잡도가
O(2^n)으로 비효율적입니다.
재귀 + 메모이제이션 (Top-down DP)
중복 계산을 방지하기 위해 메모이제이션을 적용한 방법입니다.
1
2
3
4
5
6
7
8
9
10
11
#include <bits/stdc++.h>
using namespace std;
vector<int> dp(50, -1);
int fibonacci(int n) {
if (n <= 1) return n;
if (dp[n] != -1) return dp[n];
return dp[n] = fibonacci(n - 1) + fibonacci(n - 2);
}
- 특징: 시간 복잡도를
O(n)으로 줄일 수 있으며, 추가적인O(n)공간이 필요합니다.
2. 반복적 구현 (Iterative)
순차적으로 계산을 진행하는 방법입니다.
기본 반복 구현 (공간 최적화)
1
2
3
4
5
6
7
8
9
10
int fibonacci(int n) {
if (n <= 1) return n;
int a = 0, b = 1;
for (int i = 2; i <= n; i++) {
int c = a + b;
a = b;
b = c;
}
return b;
}
- 장점: 시간 복잡도
O(n), 공간 복잡도O(1)로 매우 효율적입니다. - 단점: 이전 두 항만 기억하므로, 이미 계산된 항이라 하더라도 그 값을 즉시 조회할 수 없습니다.
반복 + 메모이제이션 (Bottom-up DP)
중복 계산을 방지하고 모든 항의 값을 미리 계산하여 배열에 저장함으로써, 이후 임의 항에 대해 즉시 접근이 가능하도록 합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <bits/stdc++.h>
using namespace std;
vector<int> dp(50, 0);
int fibonacci(int n) {
if (n <= 1) return n;
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
- 특징: 시간 복잡도
O(n), 공간 복잡도O(n)이며, 저장된 모든 항을 바로 참조할 수 있습니다.
3. 행렬 거듭제곱 (Matrix Exponentiation)
수열을 행렬 곱셈으로 표현하여 빠르게 계산하는 방법입니다.
\[\begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^n = \begin{pmatrix} F(n+1) & F(n) \\ F(n) & F(n-1) \end{pmatrix}\]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <bits/stdc++.h>
using namespace std;
typedef vector<vector<long long>> matrix;
matrix multiply(const matrix& a, const matrix& b) {
matrix res(2, vector<long long>(2));
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
res[i][j] = 0;
for (int k = 0; k < 2; k++) {
res[i][j] += a[i][k] * b[k][j];
}
}
}
return res;
}
matrix matrixPow(matrix base, int n) {
matrix res = {{1, 0}, {0, 1}};
while (n) {
if (n % 2) res = multiply(res, base);
base = multiply(base, base);
n /= 2;
}
return res;
}
long long fibonacci(int n) {
if (n == 0) return 0;
matrix base = {{1, 1}, {1, 0}};
return matrixPow(base, n - 1)[0][0];
}
- 장점: 시간 복잡도
O(log n)으로 매우 빠르며, 큰 수를 계산할 때 유리합니다. - 단점: 단위 연산량이 많아 작은
n에서는 반복적 구현보다 느릴 수 있습니다.
참고: 행렬 거듭제곱 방식에서도 계산된 중간 행렬을 메모이제이션할 수 있습니다. 그러나 일반적으로 빠른 거듭제곱 알고리듬 자체가 매우 효율적이기 때문에 별도로 메모이제이션을 적용할 필요는 거의 없습니다.
시간/공간 복잡도 요약
| 방법 | 시간 복잡도 | 공간 복잡도 |
|---|---|---|
| 재귀 | O(2^n) | O(n) |
| 재귀 + 메모이제이션 (Top-down DP) | O(n) | O(n) |
| 반복 | O(n) | O(1) |
| 반복 + 메모이제이션 (Bottom-up DP) | O(n) | O(n) |
| 행렬 거듭제곱 | O(log n) | O(log n) |
시간/공간 복잡도 그래프
아래는 재귀적 구현, 반복적 구현, 행렬 거듭제곱 방식의 시간 복잡도를 비교한 그래프입니다.
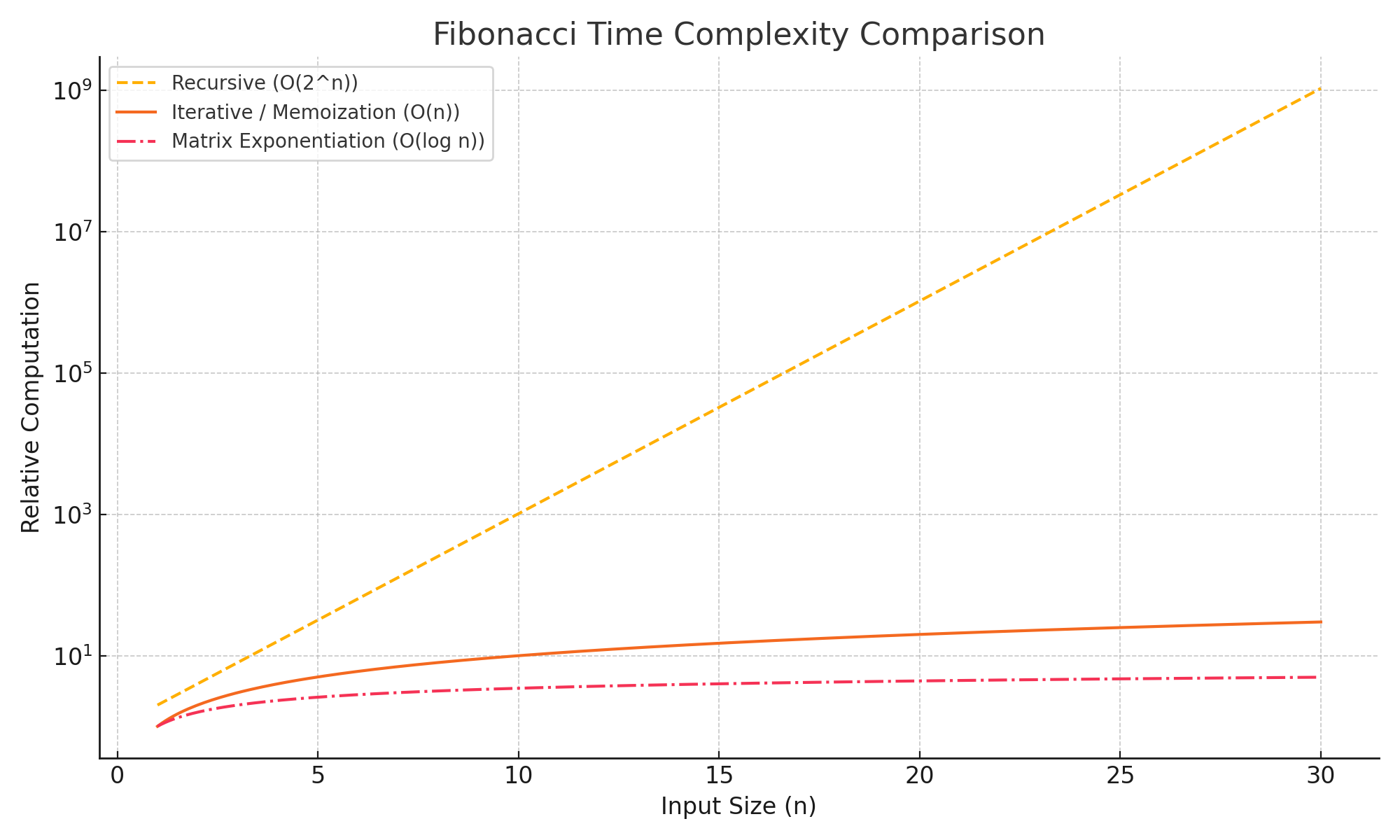
- Recursive
O(2^n): 입력 크기에 따라 급격히 기하급수적으로 증가합니다. - Iterative / Memoization
O(n): 입력 크기에 비례하여 선형적으로 증가합니다. - Matrix Exponentiation
O(log n): 매우 완만하게 증가합니다.
참고: 메모이제이션을 적용하면 재귀적 구현도
O(n)으로 최적화되기 때문에, 실제 비교는 재귀(미적용) vs 반복 vs 행렬 거듭제곱의 기본 구조 차이를 중심으로 이해하는 것이 중요합니다.
마무리
피보나치 수열은 단순한 규칙을 바탕으로 하지만, 다양한 계산 방법과 최적화 전략을 통해 수학적 사고를 확장하는 데에 도움이 되는 재밌는 수열입니다.