다익스트라 알고리즘 (Dijkstra’s algorithm) - soo:bak

작성일 :

개념

  • 벨만-포드 알고리즘 처럼, 시작 노드에서 그래프의 다른 모든 노드로 가는 최단 경로를 구하는 알고리즘

특징

  • 벨만-포드 알고리즘과의 비교
    • 장점 : 더욱 효율적이기 때문에, 그래프의 크기가 큰 경우에도 사용 가능
    • 단점 : 가중치가 음수인 간선이 없는 경우에만 사용 가능
  • 가중치가 음수인 간선의 존재를 배제한 알고리즘이기 때문에, 그래프에 있는 모든 간선을 한 번만 처리하는 것으로 효율성을 확보한 것
  • 각 노드를 처리한 뒤에는 해당 노드까지의 거리가 절대 변하지 않음

설명

  • 시작 노드 에서부터 인접한 노드까지의 최단 거리값을을 구하여 저장하고, 탐색 과정을 통하여 다른 노드들의 거리값을 줄여나감
  • 단계 구성
    • 아직 처리하지 않은 노드들 중 거리값이 가장 작은 노드에서 탐색을 시작
    • 해당 노드에서 시작하는 모든 간선을 통해 이웃 노드를 탐색
    • 만약, 방문한 이웃 노드가 아직 처리되지 않은 노드이고, 거리값을 줄일 수 있는 노드인 경우, 해당 노드의 거리값을 줄임


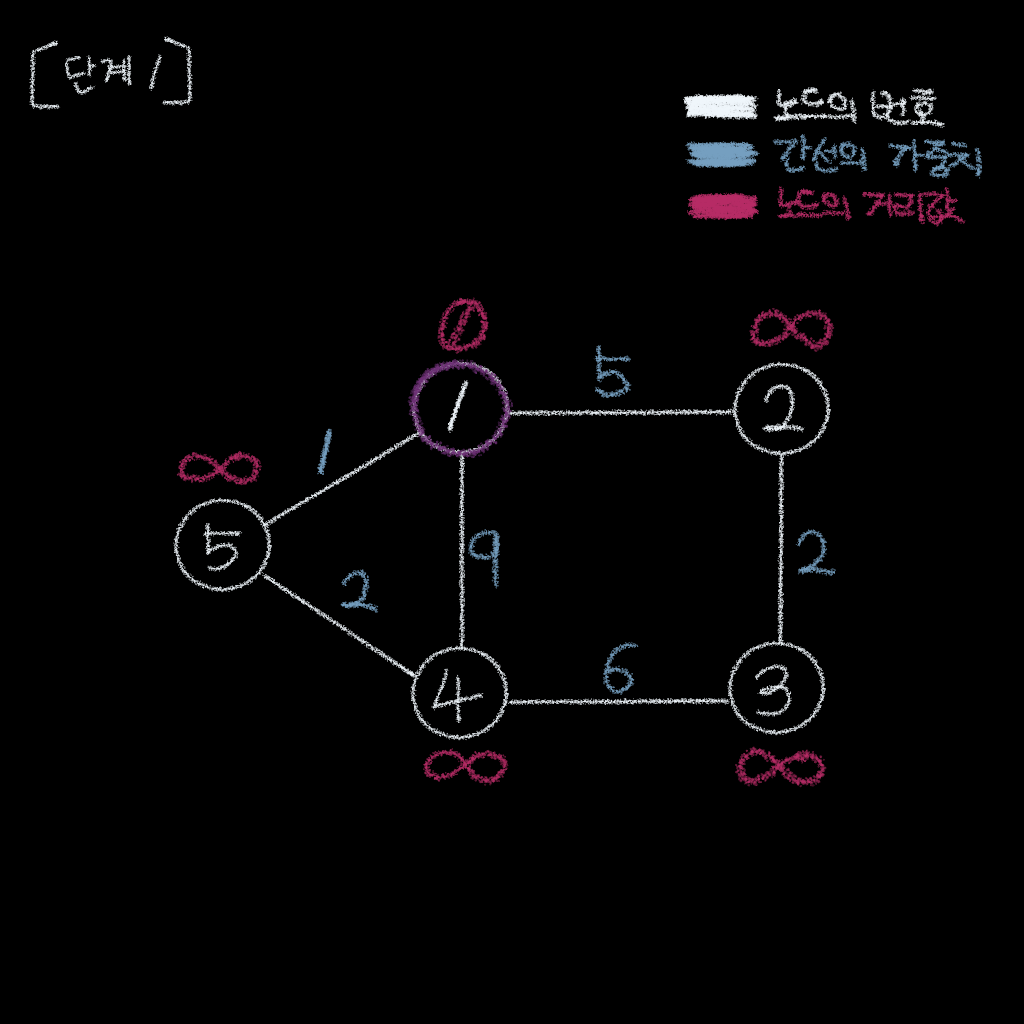단계 1

단계 1  .  노드들의 초기 거리값을 설정

  • 벨만-포드 알고리즘의 시작 단계와 동일
  • 시작 노드의 거리값은 0
  • 다른 모든 노드의 거리값은 무한대




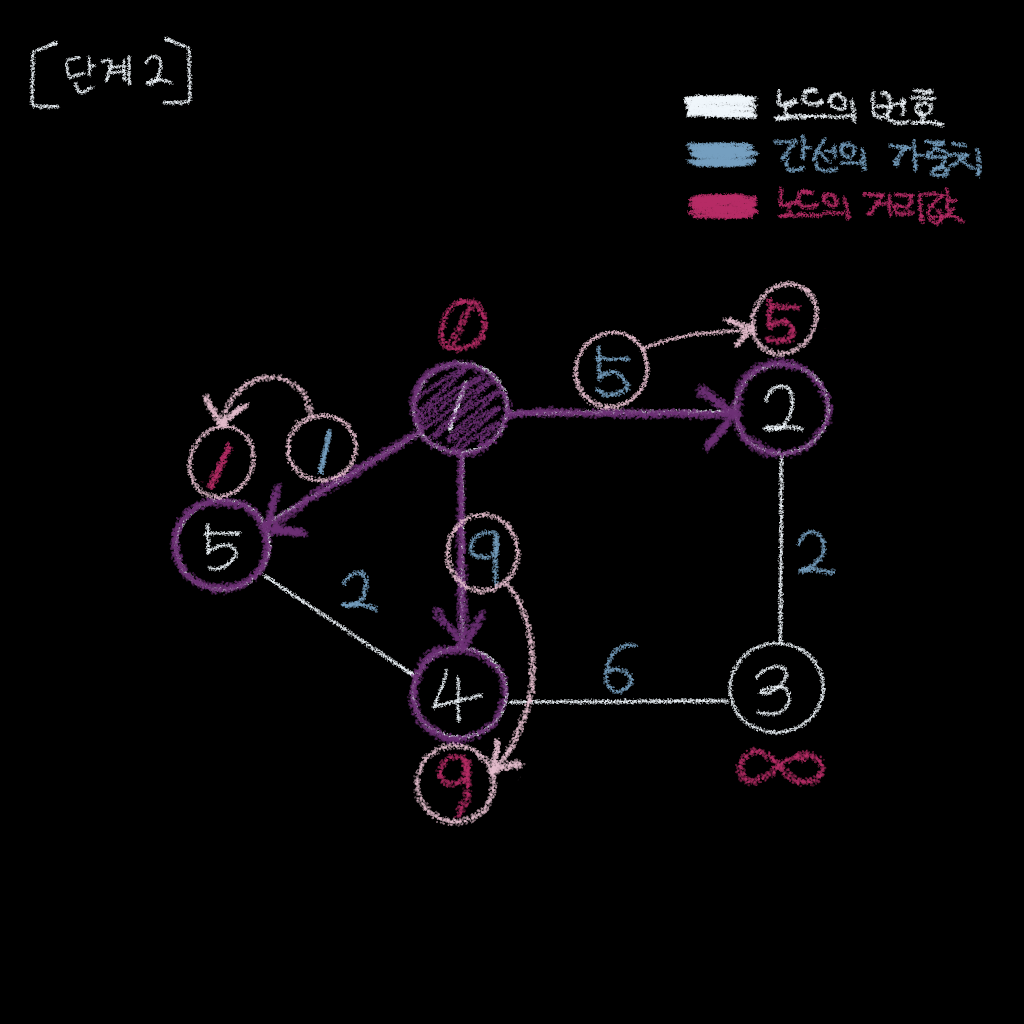단계 2

단계 2  .  시작 노드로부터의 간선들을 이용하여, 연결되는 노드들의 거리값을 줄임

  • 노드 1   ->  노드 2   간선의 거리는 5 이므로, 노드 2 의 거리값은 5
  • 노드 1   ->  노드 4   간선의 거리는 9 이므로, 노드 4 의 거리값은 9
  • 노드 1   ->  노드 5   간선의 거리는 1 이므로, 노드 5 의 거리값은 1




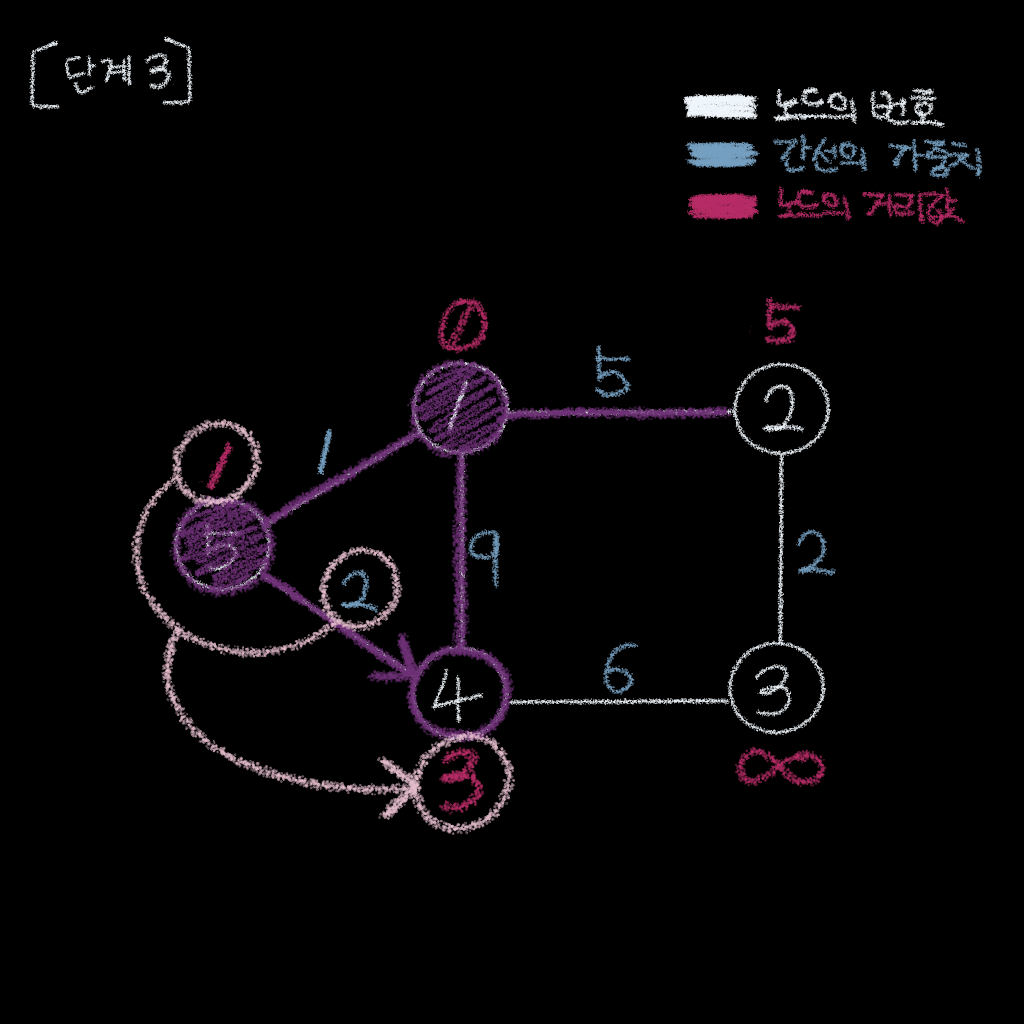단계 3

단계 3  .  아직 인접 간선을 처리하지 않은 노드들 중, 거리값이 가장 작은 노드인 노드 5   를 방문

현재 노드 5  의 거리값 = 1

  • 노드 5   에서 시작되는 간선을 이용하여, 아직 방문하지 않은 이웃 노드들의 거리값을 줄임
  • 현재 노드 5 의 거리값은 1 이며,  노드 5   ->   노드 4   간선의 거리는 2
  • 즉, 총 거리 합은 3
  • 따라서, 기존 노드 4   의 거리값을 9 에서 3 으로 줄일 수 있음




단계 4

단계 4  .  아직 인접 간선을 처리하지 않은 노드들 중, 거리값이 가장 작은 노드인 노드 4   를 방문

현재 노드 4  의 거리값 = 3

  • 현재 노드 4 의 거리값은 3 이며,  노드 4   ->   노드 3   간선의 거리는 6
  • 즉, 총 거리 합은 9
  • 따라서, 기존 노드 3   의 거리값을 무한대 에서 9 로 줄일 수 있음




단계5

단계 5  .  아직 인접 간선을 처리하지 않은 노드들 중, 거리값이 가장 작은 노드인 노드 2   를 방문

현재 노드 2  의 거리값 = 5

  • 현재 노드 2 의 거리값은 5 이며,  노드 2   ->   노드 3   간선의 거리는 2
  • 즉, 총 거리 합은 7
  • 따라서, 기존 노드 3   의 거리값을 9 에서 7로 줄일 수 있음




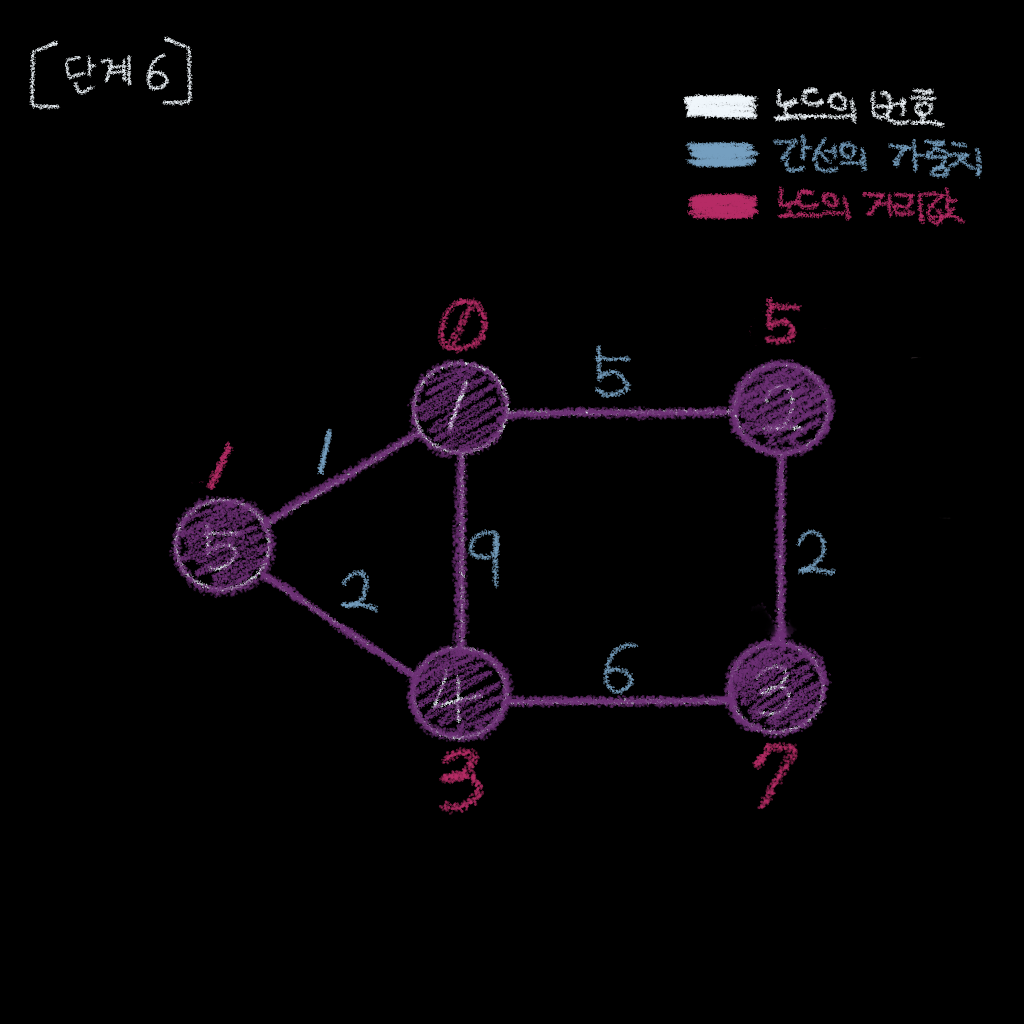종결

모든 노드들을 방문하였으므로 종결


구현

  • 그래프는 보통 가중치가 포함된 간선 리스트를 이용
  • 아직 처리하지 않은 노드들 중 거리값이 최소인 노드를 효율적으로 탐색해야 함
  • 이를 위해 아직 처리하지 않는 노드를 거리 기준으로 저장하는 우선순위 큐를 적절한 자료구조로 선택
  • 교과서적인 다익스트라 알고리즘의 구현에서는 원소의 값을 수정할 수 있는 우선순위 큐를 사용
    • 이런 경우, 각 노드에 대응되는 원소를 큐에 한 번씩만 저장하면 되고, 필요한 경우에 원소가 저장하고 있는 값(이 알고리즘에서는 거리값)을 수정하면 되므로 편리함
  • 하지만 C++의 STL 에 있는 우선순위 큐에는 그러한 연산이 없기 때문에, 보통 다른 구현 방식을 사용
    • 거리가 바뀔 때 마다, 해당하는 노드를 우선순위 큐에 새롭게 추가하는 방식
    • 우산순위 큐를 pair<int, int> 자료형을 담을 수 있도록 생성하고, (-dist, nodeX) 의 형태로 값을 저장

      nodeX 까지의 거리가 dist 임을 의미

      dist 에 음수 값을 취한 이유는 C++ 의 STL 에서 기본 버전의 우선순위 큐는 최대 원소 를 찾도록 되어 있지만, 다익스트라 알고리즘에서는 최소 원소 를 구해야 함.
      이를 해결하기 위해 비교 함수를 추가로 구현하는 것 보다, 간단하게 거리 값에 음수 값을 취해줌으로써 우선 순위 큐의 기본 버전 사용이 가능

    • 같은 노드에 대하여 여러 원소들이 우선순위 큐에 저장될 수 있지만, 그 중 거리값이 최소인 원소 만 처리된다는 점이 중요 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

typedef pair<int, int> pii;

void dijkstra(int nodeStart) {
  for (int i = 1; i <= n; i++) {
    dist[i] = INFINITY;
    isVisited[i] = false;
  }

  dist[nodeStart] = 0;
  priority_queue<pii> pq;

  pq.push({0, nodeStart});
  while (!pq.empty()) {
    int nodeCur = pq.top().second;
    pq.pop();

    if (isVisited[nodeCur]) continue ;
    isVisited = true;

    for (auto u : adj[nodeCur]) {
      int nodeNext = u.first, w = u.second;
      if (dist[nodeNext] > dist[nodeCur] + w) {
        dist[nodeNext] = dist[nodeCur] + w;
        pq.push({-dist[nodeNext], nodeNext});
      }
    }
  }
}



이 블로그의 다른 글