플로이드-워셜 알고리즘 (Floyd-Warshall algorithm) - soo:bak

개념

• 벨만-포드 알고리즘, 다익스트라 알고리즘과 다르게, 한 번의 실행으로 모든 노드들 간의 최단 경로를 구할 수 있는 알고리즘
• 이 알고리즘에서는 노드들 간의 거리를 저장하기 위해 행렬 을 사용하며, 행렬의 초깃값은 그래프의 인접 행렬의 값과 같음
  
• 알고리즘은 여러 라운드로 구성
  • 각 라운드마다 중간 노드 로 사용할 노드를 선택하여, 해당 노드와 인접하는 노드들을 잇는 연결 거리값을 구하여 행렬에 저장
    
    
    

특징

• 플로이드-워셜 알고리즘은 3중으로 중첩된 반복문 으로 구성되어 있고, 각각은 그래프의 노드 수 만큼 반복을 하므로, 시간 복잡도는  O(n³)
• 구현이 간단하기 때문에, 그래프에서 한 쌍의 노드 사이의 최단 경로만 구하려 할 때에도 이 알고리즘을 사용할 수 있음
  • 단, 그래프의 크기가 작아서 세 제곱 시간 알고리즘으로도 해결이 가능한 경우에만 가능
    
    
    

설명

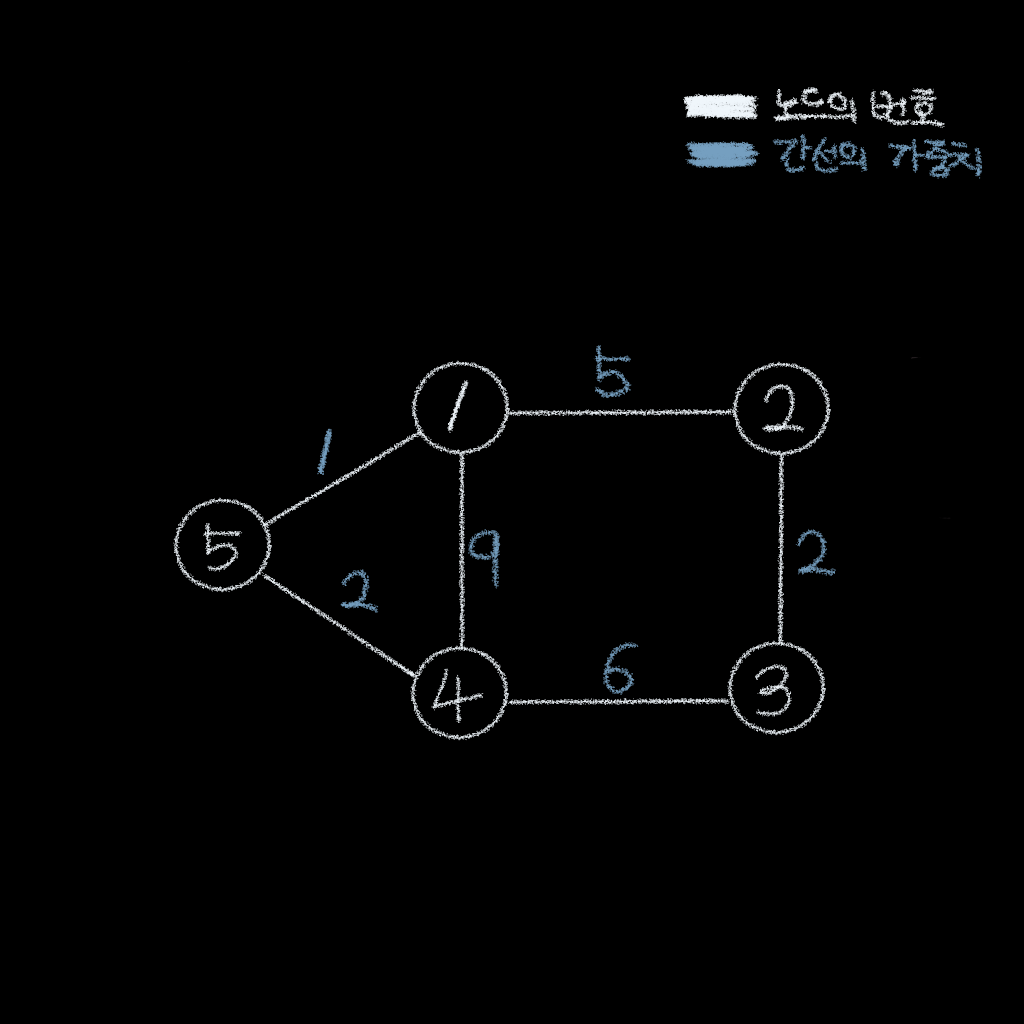예시 그래프

단계 1  .  노드들의 초기 거리값을 행렬에 저장
그래프가 위의 그림과 같이 입력되었을 때, 행렬의 초깃값은 다음과 같음

행렬의 초깃값

단계 2  .  첫 번째 라운드

• 임의로 1번 노드 를 첫 번째 라운드의 중간 노드 로 선택, 해당 노드와 인접하는 노드들을 이어 경로의 거리값을 구하여 저장
  
  • 2번 노드 와 4번 노드 를 잇는 길이가 14 인 경로를 만들 수 있음
    
  • 2번 노드 와 5번 노드 를 잇는 길이가 6 인 경로를 만들 수 있음
    
  • 결과를 다음과 같이 배열에 저장
    

  1번 노드를 중간노드로 활용한 결과

단계 3  .  두 번째 라운드

• 아직 중간 노드 로 활용되지 않은 노드들 중 임의로 2번 노드 를 두 번째 라운드의 중간 노드 로 선택
  
  • 1번 노드 와 3번 노드 를 잇는 길이가 7 인 경로를 만들 수 있음
    
  • 1번 노드 와 5번 노드 를 잇는 길이가 8 인 경로를 만들 수 있음
    
  • 결과를 다음과 같이 배열에 저장
    

  2번 노드를 중간노드로 활용한 결과

이와 같은 방식으로 모든 노드가 중간 노드로 선정될 때 까지 라운드를 계속 반복하여 진행

• 알고리즘이 종료되고 나면, 행렬에는 모든 노드들 간의 최단 거리가 저장되게 됨
  

  최종 결과
  

• 예를 들면, 최종 행렬을 통해 2번 노드와 4번 노드 간의 최단 경로는 8 임을 알 수 있음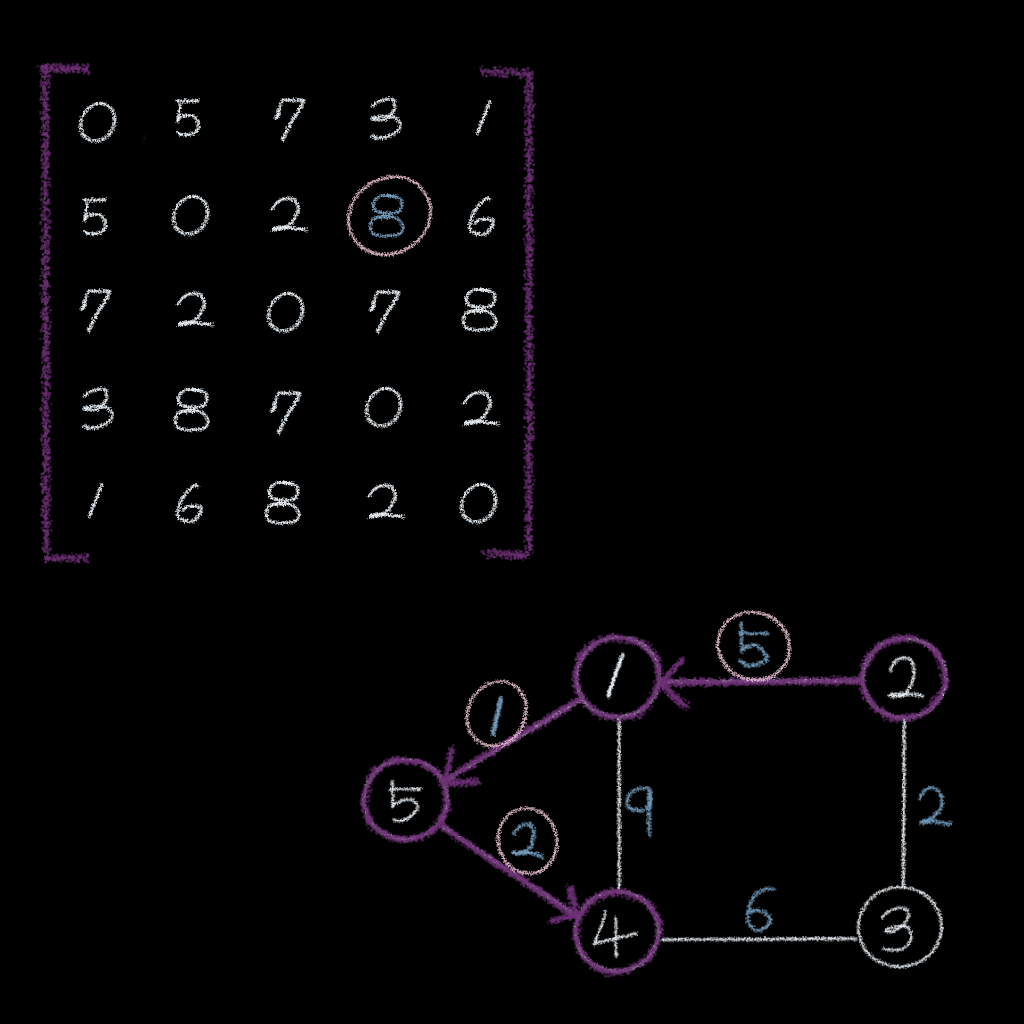
  

  2번 노드와 4번 노드 사이의 최단 경로는 8
  
  
  

구현

• 먼저 dist 배열 (행렬)을 adj (그래프의 인접 행렬)을 이용하여 초기화
  

for (int from = 1; from <= n; from++) {
  for (int to = 1; to <= n; to++) {
    if (from == to) dist[from][to] = 0;
    else if (adj[from][to]) dist[from][to] = adj[from][to];
    else dist[from][to] = INFINITY;
  }
}

• 초기화 이후, 알고리즘 구현
  

for (int via = 1; via <= n; via++) {
  for (int from = 1; from <= n; from++) {
    for (int to = 1; to <= n; to++) {
      dist[from][to] = min(dist[from][to], dist[from][via] + dist[via][to]);
    }
  }
}